Have you ever been fooled by statistics? Simpson’s paradox shows how analyzing data in total can obscure important trends. We can uncover hidden factors that reverse or eliminate relationships by breaking down information. This short guide will equip you to avoid being misled by aggregated data and ensure you see the whole picture.

Simpson’s Paradox is a statistical phenomenon. It occurs when trends in subgroups disappear or reverse in combined data. This paradox can lead to misleading conclusions. It’s crucial in data analysis across many fields. Examples include medical research and social sciences. The paradox affects how we interpret study results. It shows why examining subgroups is important. Analysts must look beyond overall trends. They need to consider underlying factors. Simpson’s Paradox reminds us that data can be complex. It highlights the need for thorough statistical analysis. Understanding this concept helps prevent incorrect interpretations of data.
Let’s understand Simpson’s Paradox better with some examples!
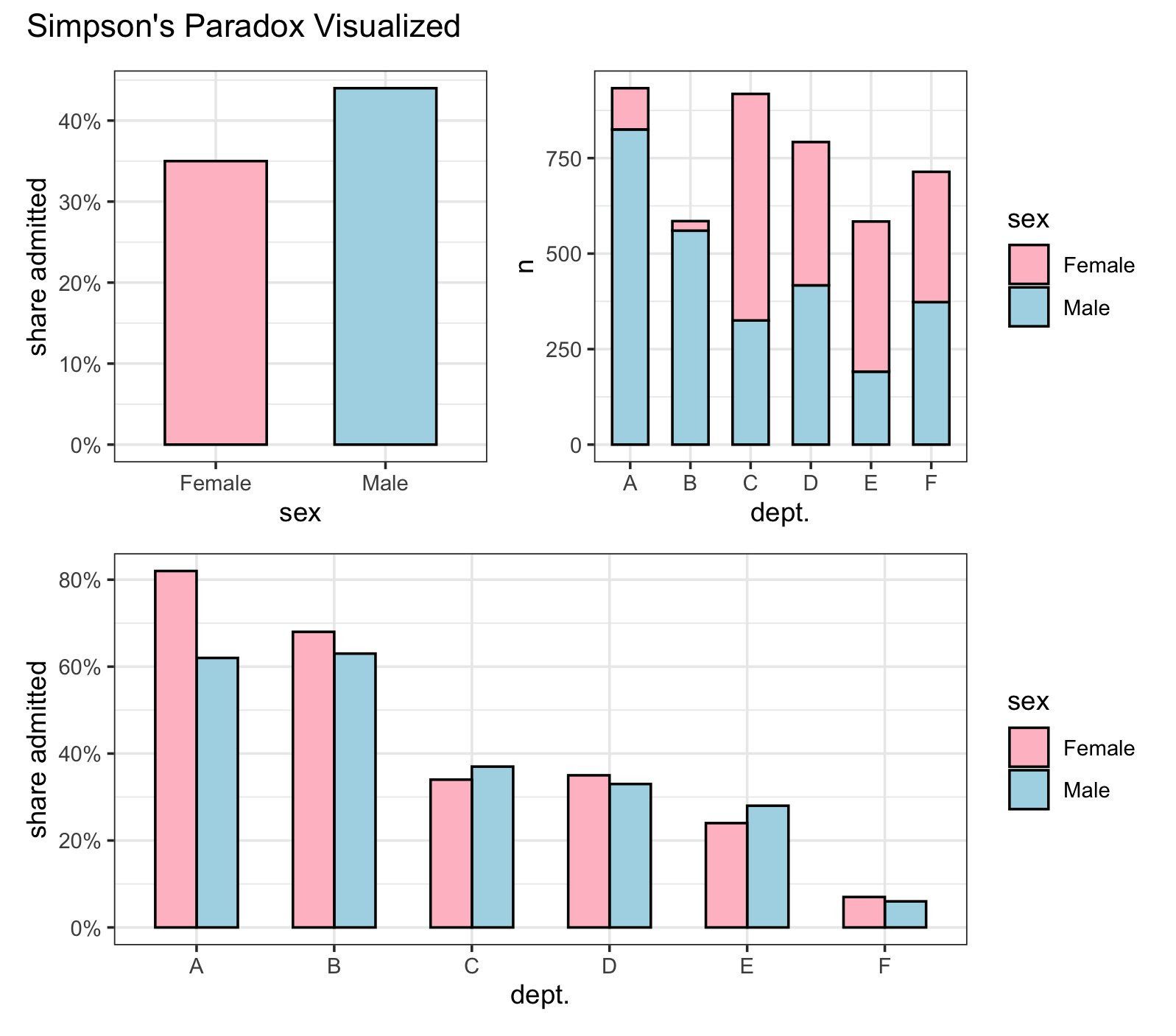
One of the most famous examples of Simpson’s Paradox is the UC Berkeley gender admissions case. Initially, male applicants appeared to have a significantly higher acceptance rate than female applicants, suggesting possible gender bias. The aggregated data showed:
However, upon disaggregating the data by department, a different picture emerged. Women tended to apply to more competitive departments with lower acceptance rates, whereas men applied to departments with higher acceptance rates. When analyzing the data within each department, the gender bias disappeared, and in some cases, women had higher acceptance rates than men. This demonstrates how data aggregation can obscure the true relationship between variables.
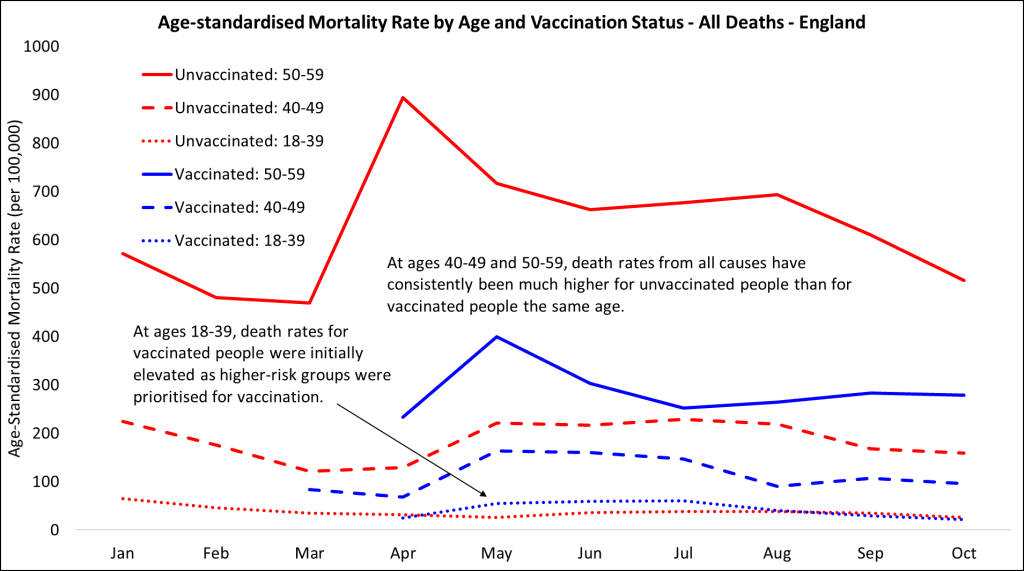
During the COVID-19 pandemic, data showed that a higher percentage of vaccinated individuals died from COVID-19 compared to unvaccinated individuals. This initially seemed counterintuitive and raised questions about the efficacy of vaccines. However, this was another instance of Simpson’s Paradox.
The vaccinated population tended to be older and had more underlying health conditions, both of which are risk factors for severe COVID-19 outcomes. When adjusting for age and health status, it was evident that vaccinated individuals had a significantly lower risk of dying from COVID-19 compared to their unvaccinated counterparts. This example underscores the necessity of considering confounding variables to draw accurate conclusions from data.
Simpson’s Paradox typically arises due to a confounding variable affecting the relationship between the primary variables of interest. This confounding variable can create a misleading picture when data is aggregated. Here are some key reasons why Simpson’s Paradox occurs:
Also Read: What is Data Analytics? How to Use it in Your Career?
Let’s look at some use cases of Simpson’s Paradox. These cases demonstrate why examining data from multiple perspectives is crucial. The overall numbers don’t always tell the full story.
Medical Trials: The Tricky Drug
A new pain relief drug shows:
Looks promising. But closer inspection reveals:
The drug is 10% more effective in each group, not just overall. This discrepancy occurred because more seniors were in the trial, lowering the average. Without this analysis, we’d miss its effectiveness for younger groups.
Voting: The Popular Vote Puzzle
Scenario:
Final tally:
If each state is worth one “point,” Purple could win more states and the election despite fewer total votes.
For instance, in 2016, Clinton received 2.9 million more votes than Trump overall, yet Trump won more states and the presidency.
These cases demonstrate why examining data from multiple perspectives is crucial. The overall numbers don’t always tell the full story.
Also Read: Step-by-Step Exploratory Data Analysis (EDA) using Python
Don’t let Simpson’s Paradox fool you! Here’s what to do:
Remember, the devil’s in the details. Follow these tips, and you’ll be a data detective in no time!
Simpson’s Paradox shows us how tricky data can be. It’s like a magic trick that reminds us to look closer. Don’t just trust the big picture—dig into the details. It tells us to watch out for hidden factors that might change everything. We can avoid jumping to wrong conclusions by keeping this paradox in mind. It helps us see what’s going on in our data, not just what it looks like at first glance.
Read more about the Simpson’s Paradox here – Stanford Research
Ans. Simpson’s paradox occurs when a trend in separate groups reverses when the data is combined. It’s like seeing apples win in one basket and oranges in another, but bananas are suddenly on top when you mix all fruits. It shows how grouping data can change conclusions.
Ans. To spot Simpson’s paradox, compare trends in subgroups to the overall trend. Look for reversals or significant changes when data is combined or split. Analyze data at different levels and watch for inconsistencies. Be aware of group sizes and potential hidden variables that might influence results.
Ans. Simpson’s paradox is when grouped data shows one trend, but the combined data shows another. To avoid it, always examine data at multiple levels. Consider confounding variables and group sizes. Don’t rush to conclusions based on aggregated data alone. Question your assumptions and look for alternative explanations.
Ans. The logic behind Simpson’s paradox lies in how data is distributed and combined. Unequal group sizes or overlooked variables can skew overall results. It shows that relationships between variables can change depending on how we slice the data. This paradox reminds us that context matters in data interpretation.
Lorem ipsum dolor sit amet, consectetur adipiscing elit,